Nonlinear MPC for Bipedal Locomotion

Projects | 2022 | Links: Link

In this project I explored and developed The ability to generate dynamic bipedal walking in real-time for bipedal robots with input constraints and underactuation has the potential to enable locomotion in dynamic, complex and unstructured environments. Yet, the high-dimensional nature of bipedal robots has limited the use of full-order rigid body dynamics to gaits which are synthesized offline and then tracked online. As part of my master thesis I explored, developed and sucessfully tested an online nonlinear model predictive control approach that leverages the full-order dynamics to realize diverse walking behaviors. Additionally, building up on prior work of Noel Csomay-Shanklin we coupled this approach with offline synthesized gaits to enable a shorter prediction horizon and rapid online re-planning.

The following discussion is meant to give a quick overview of the methodology employed in the paper: Planar Bipedal Locomotion with Nonlinear Model Predictive Control: Online Gait Generation using Whole-Body Dynamics.

Paper Poster Presentation Slides Experimental Results Presentation - Humanoids 2022

Presentation - Dynamics Walking 2022

Reparametriced Whole-Body MPC

Due to the computational cost of optimizing a policy online using MPC most approaches so far have relied on simplified (Linear Inverted Pendulum, Spring-Loaded Inverted Pendulum, Single Rigid Body, ect.) or reduced models (Center of Mass Dynamics). Although these simplified/reduced models can achieve impressive performance for bipedal locomotion they also have their downsides. In particular, their capability to leverage the true nonlinear dynamics and underactuation is limited and they can not take dynamics constraints such as actuator torque limits into account. Furthermore, since they produce a simplified policy they need to be combined with a Whoole-Body Controller to control the robot in torque mode.

Therefore, I started to explore the possibility to extend existing MPC frameworks by planning directly over the Whole-Body Dynamics. For this I proposed the use of a reparametrication of the whole-body dynamics that optimized directly over the joint accelerations $\ddot{\bm q_j}$.

The MPC system dynamics are defined as follows:

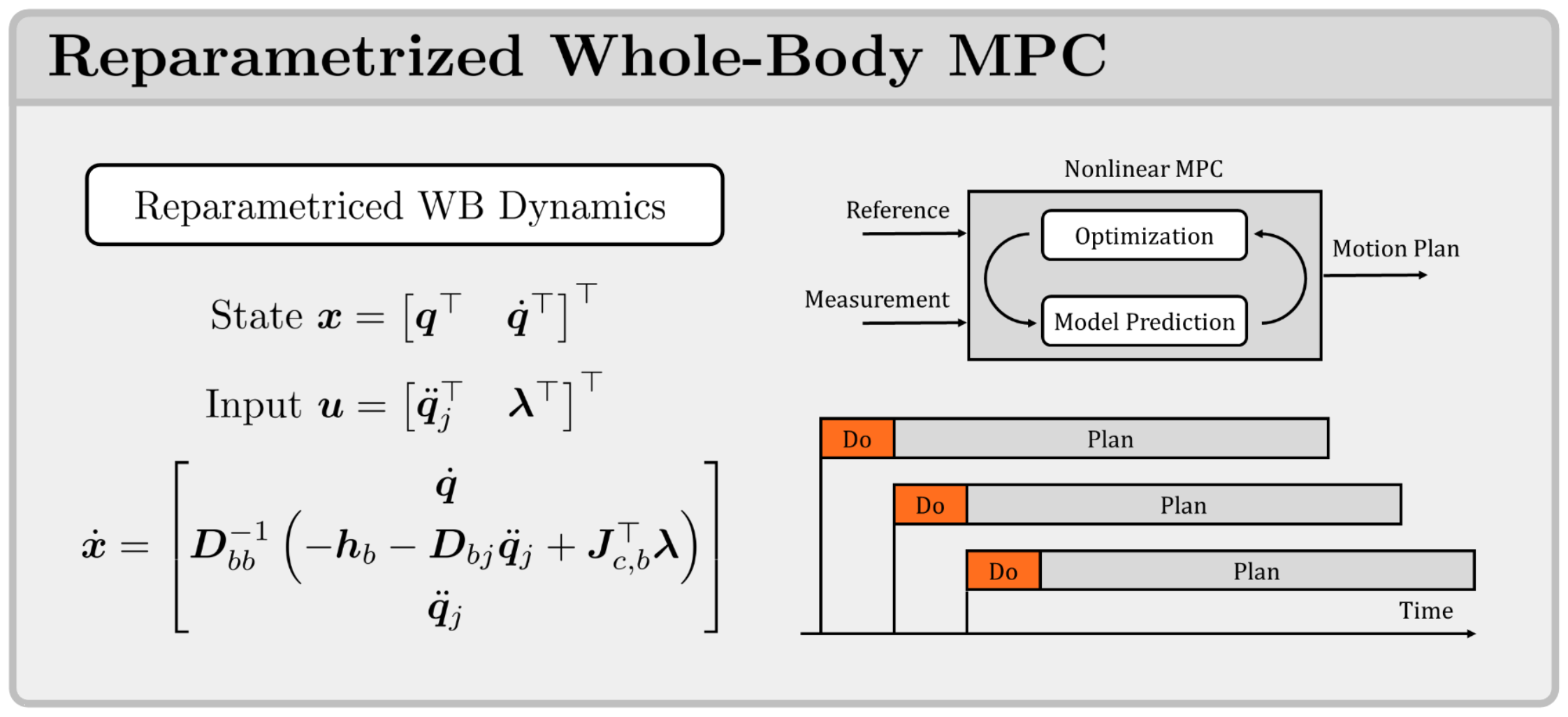
Where $\bm q$, $\ddot{\bm q_j}$, $\ddot{\bm q_j}$ and $\bm \lambda$ are the generalized coordinates, generalized velocities, generalized joint accelerations and external contact forces. As can be seen, this reparametrication focusses most of the computational complexity on the underactuated dynamics. Furthermore by excluding the Inverse Dynamics from the model prediction step the computation of the generalized mass matrix $\mathbf{D(\bm q)}$, the nonlinear effects $\bm{h}(\bm q, \dot{\bm{q}})$ and the contact Jacobian $\mathbf{J}_{c}$ can be limited to the first 6 components that influence the dynamics of the base link. Furthermore, due to the partially (block) diagonal nature of the generalized mass matrix corresponding to the base $\mathbf{D_{bb}}(\bm q) \in \mathbb{R}^{6 \times 6}$ the effectively needed to compute invers in only of dimensionality $\mathbb{R}^{3 \times 3}$

Despite those computational benefits, there is actually no loss of information and the planned joint torques can simply be recovered through inverse dynamics for every point along the planning horizon: $$\bm{\tau} = \mathbf{D}(\bm q)\ddot{\bm q}+\bm{h}(\bm q, \dot{\bm{q}}) - \mathbf{J}_{c}(\bm q)\bm{\lambda}$$

This way is is possible to add for example a torque limit to the optimization. By doing this as a part of the “sensitivity analysis” of the MPC problem, instead of in a single shooting model prediction step (as done for example in Differential dynamic programming), this computation can be parallelized.

The proposed MPC is then combined with a low level controller that recovers the planned torques and accounts for model missmath through an additional feedback term.

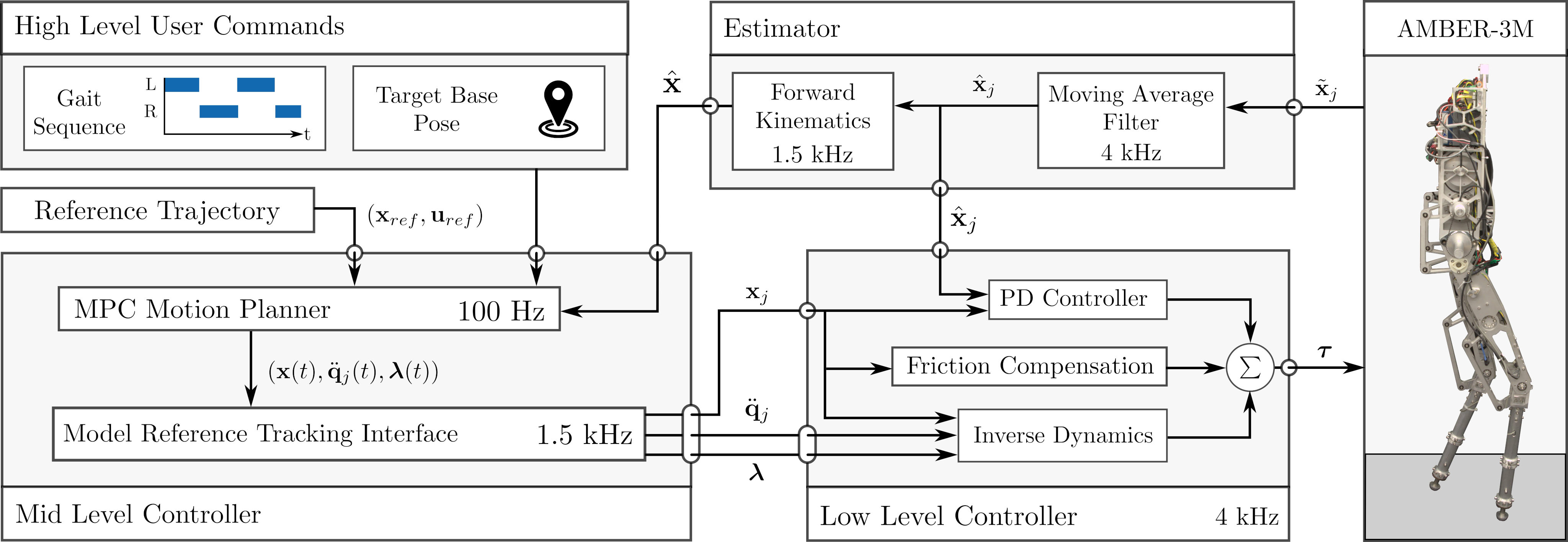
Combination with offline generated Hybrid Zero Dynamics Gaits

I am still working on documenting this part.

Experimental Results

Paper Submission Results Video

The video is rather rushed due to the time limit of the conference submission, but it highlights the most important experimental results.