Data Driven Dynamics Modelling for Unmanned Aerial Vehicles

Projects | 2021 | Links: Link

A dynamics model is a valuable tool for a variety of applications, including simulations and control. However, traditional methods for obtaining such models for an unmanned aerial vehicle (UAV), such as wind tunnel testing or the installation of additional sensors, can be time-consuming, inaccessible and costly. In this project, I aimed to address this challenge by proposing a data-driven dynamics modeling pipeline. The primary objective was to establish a PX4 compatible framework, suitable for different types of UAVs including multi-rotors, fixed-wings and VTOLs and model structures. The dynamics model of choice is obtained by minimizing the prediction error of the model with respect to the flight data collected by the by default on the vehicle installed sensors from the ULog File Format. Specifically, for the example of multi-rotors, the pipeline automates the estimation of a parametric dynamics model and integrates it into the PX4 Gazebo flight simulator.The data-driven-dynamics pipeline is published as an open source project on Github and presented at the Linux Foundation PX4 Developer Summit 2021.

Code Student Paper Presentation - PX4 Dev Summit 21

Overview of the Pipeline

The data-driven dynamics pipeline is implemented in python and consists of the following main modules:

Fig.1 - Main building blocks of the data-driven-dynamics pipeline.

• Data Processing: Responsible to load and pre-process the data used to estimate the dynamics model. It contains functionalities to filter, re-sample and normalize the data.
• Data Selection Optionally the user has the ability to visualize the data and additional step to visually select a sub-portion of the data that is best suited to estimate the dynamics model.
• Model Definition Contains the model structure used to predict the dynamics. A selection of parametric models pertaining to fundamental components, such as rotors and wings, is available and can be utilized to construct a model tailored airframe. The framework is not limited to a specific methodology and can be extended to incorporate model-free or deep learning approaches.
• Optimization Framework Interfaces the chosen model and a cost function with an optimization framework. Currently supported optimization frameworks include cvxpy and the sklearn linear regressor.
• Dynamics Model Output The output of the parametric model is automatically saved onto a YAML file that is then used to integrate the estimated dynamics into Gazeboo via a C++ plugin.

Dynamics model for UAVs

Unmanned Aerial Vehicles (UAVs) can be modeled as dynamic systems, and their behavior can be described using mathematical models that capture the underlying physics. The single rigid body dynamics (SRBD) model assumes that the UAV is a rigid body that has six degrees of freedom (3 linear and 3 rotational), and it can be modeled using the following equations: $$\dot{\bm x} = \frac{d}{dt} \left(\begin{array}{c} _{\mathcal{I}}{\mathbf{r}} \\ {\bm{\xi}}_{\mathcal{I}\mathcal{B}} \\ {_{\mathcal{B}}}{\mathbf{v}} \\ {_{\mathcal{B}}}{\bm{\omega}} \end{array}\right) = \left(\begin{array}{c} {\mathbf{R}}_{\mathcal{I}\mathcal{B}} \cdot {_{\mathcal{B}}}\mathbf{v} \\ \bm{\chi}^{-1} \bm{\omega} \\ \frac{1}{m} {\mathbf{R}}_{\mathcal{I}\mathcal{B}} \cdot { _{\mathcal{B}}}\mathbf{F} + _{\mathcal{I}}\mathbf{g} \\ {_{\mathcal{B}}}\mathbf{I}^{-1} ({_{\mathcal{B}}}\mathbf{M} - {_{\mathcal{B}}}\bm{\omega}^{} \times {_{\mathcal{B}}}\mathbf{I} \cdot {_{\mathcal{B}}}\bm{\omega}) \end{array}\right)$$

where the state vector $\bm x \in \in \mathbb{R}^13$ contains the position vector $\mathbf{r} \in \mathbb{R}^3$, the unit quaternion $\boldsymbol{\xi}_{\mathcal{I}\mathcal{B}} \in \mathbb{S}^4$ and the linear and anular velocity vectors $\mathbf{v} \in \mathbb{R}^3$ and $\mathbf{\omega} \in \mathbb{R}^3$ respectively. ${\mathbf{R}}_{\mathcal{I}\mathcal{B}} \in \mathbb{R}^{3 \times 3}$ is the rotation matrix representing the rotation from body frame $\mathcal{B}$ into inertial frame $\mathcal{I}$, $\mathbf{F} \in \mathbb{R}^3$ is the net aerodynamic force acting on the body, $\mathbf{g} \in \mathbb{R}^3$ is the gravitational force, $\mathbf{M} \in \mathbb{R}^3$ is the net moments acting on the body, $m \in \mathbb{R}$ is the mass of the body, and $\mathbf{I} \in \mathbb{R}^{3 \times 3}$ is the inertia tensor of the body.

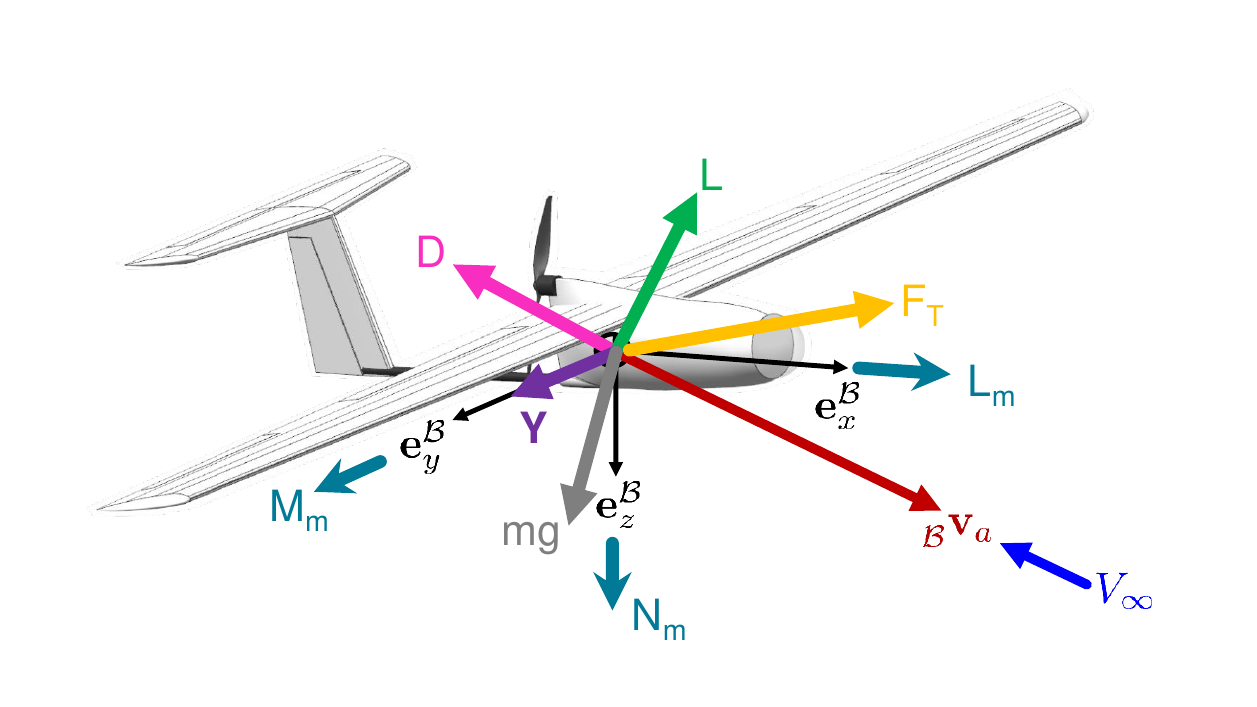
Fig.1 - Forces and moments applying on fixed-wing UAV (by Thomas Stastny).

As can be seen in equation $(1)$ the main unknowns that need to be determined are the aerodynamic forces (e.g. thrust, lift, drag) and moments (roll, pitch and yaw) and inertia tensor. Alternatively to estimating those separately it is also possible to directly estimate the the linear and angular acceleration, which practically lumps the estimation of the moments and inertia tensor together.

Model Fit

Parametric Model

For the parametric model a set of optimal parameters is obtained by minimizing the prediction error of the model $f(\bm{x}, \boldsymbol{\theta})$ using the measurement $\bm x$ and output $\bm y$ for each recorded data point $n$. $$\boldsymbol{\hat{\theta}} = \underset{\boldsymbol{\theta}}{\mathrm{argmin}} ; \frac{1}{n} \sum_{i=1}^n || \bm{y}_i - f(\bm{x}_i, \boldsymbol{\theta})||_2$$

To estimate dynamics for UAVs the outputs $\bm y$ typically include the measured linear and angular accelerations as the main uncertainties. But it is also possible to extend this to include a penalization of measured and predicted velocities or poses of the UAV.

A hand-crafted parametric model has several advantages. This model choice provides a high degree of control over its fidelity, facilitating the collection of a dataset that contains all the information needed to estimate the chosen model. Moreover, it allows us to quantitatively estimate how much information on a certain parameter is present in the data set. For a model that is linear with respect to its parameters (but potentially nonlinear with respect to its state $\bm x$ or input $\bm u$) a closed form solution to the above problem (linear least squares problem) using for example the included sklearn linear regressor. For a more complex model that is nonlinear in the parameters the solution can be obtained through cvxpy for convex problems and the scipy minimizer for non-convex problems. However, this can be readily expanded to a model-free or deep learning methodology.

Model Choice & Data Quality

Throughout the course of my research, I came to realize that the primary obstacle in estimating UAV dynamics lies not in the actual modeling of the dynamics but rather in obtaining and verifying an appropriate dataset. For accurate estimation of a UAV’s dynamics, the dataset must capture all the relevant physical effects independently and adequately covers of the state input-space of the system. Otherwise, significant discrepancies in the estimated dynamics model will be observed when evaluated beyond the distribution of the training data. Furthermore, external effects such as wind conditions

Therefore, even for a relatively uncomplicated platform such as a multi-rotor, an organized methodology for gathering and validating data is paramount to the attainment of a comprehensively generalizable model that faithfully captures the underlying physical phenomena. The challenge of selecting an appropriate dataset becomes even greater for fixed-wing and vertical take-off and landing (VTOL) UAVs, as they exhibit highly nonlinear behavior and instability near the stall. This necessitates the development of specialized flight maneuvers that explore the dynamics beyond their nominal operating point and potentially outside if the vehicles narrow stability range (e.g. post stall regime).

For a model that is linear with respect to its parameters the quality of the estimated parameters can be computed through a significance test and correlation matrix. those methods however, do not generalize to a nonlinear parametric model.

Assessment of Data Quality via Fisher Information

Through the computation of Fisher information an estimate of how much information data provides for estimating a parameter $\theta$. This is achieved via a first and second order sensitivity analysis w.r.t $\theta$ of the logarithmic likelihood to observe measurement X given parameter value. Intuitively, if the logarithmic likelihood function is sharply peaked with respect to changes in parameters $\bm \theta$, it is easy to indicate the “correct” value of $\bm \theta$ from the data. $$\bm s( \bm \theta) = -\mathbb{E}\left[\frac{\partial \log f(\bm X; \bm \theta)}{\partial \bm \theta}\right ]$$

Where $f(\bm X; \bm \theta)$ is the probability density function of observing the random variable $\mathbf{X} = [\mathbf{x}_0, ..\mathbf{x}_n]^T$ given the parameter $\theta$, and $\mathbb{E}$ denotes the expected value operator.

Given that the log-likelihood is continuous it can be shown that the score vanishes at maximum likely choice of $\bm \theta$. The fisher information is defined as the variance of the score/informant, which corresponds to the curvature of the log-likelihood function. $$\bm I( \bm \theta) = -\mathbb{E}\left[\frac{\partial^2 \log f(\bm X; \bm \theta)}{\partial \bm \theta^2}\right]$$

where $I(\theta)$ is the Fisher information matrix with respect to the parameter $\theta$.

Fisher Information of Linear Model

For a linear model $y = \bm x^T \bm \theta + \epsilon$ under the assumption of zero mean gaussian distributed measurement noise $\epsilon$ the output we would like to predict ($y$) becomes itself a gaussian distributed value with mean $\mu = \bm x_i^T \bm \theta$ and variance $\sigma$. $$L(\boldsymbol{\beta} | \mathbf{y}, \mathbf{X}) = \frac{1}{(2\pi\sigma^2)^{n/2}} \exp\left(-\frac{1}{2\sigma^2} \sum_{i=1}^{n} (y_i - \mathbf{x}_i^T \boldsymbol{\beta})^2\right) \\[2em] log(L(\boldsymbol{\beta} | \mathbf{y}, \mathbf{X})) = -\frac{n}{2} \log(2\pi\sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^{n} (y_i - \mathbf{x}_i^T \boldsymbol{\beta})^2$$

From this it can easily be seen that the Fisher Information simply becomes: $$\bm I( \bm \theta) = \frac{1}{2\sigma^2} \sum_{i=1}^{n} \mathbf{x}_i \mathbf{x}_i^T = \frac{1}{2\sigma^2} \mathbf{X}^T \mathbf{X}$$

Importantly it can be seen, that the information contained about each parameter $\theta$ in $\mathbf{x}_i$ is proportional to $\bm I_i = \mathbf{x}_i \mathbf{x}_i^T$. Furthermore, in case $\bm I_i$ is not of full rank the sample contains no information on the parameters corresponding to the zero eigenvalues. Those properties build the basis for a theoretically thorough and generalizable automatic data selection.

Resources

Presentation at the PX4 Developer Summit 2021